| Téma: Matematika |
|
|
| katáng |
|
a),b),c) következtetéseid helyesek, innen kellene folytatni.
piros + kék + fehér + kék + fehér + piros = 132 db
Vajon a piros + kék + fehér összege mennyi? A 100-ból kivonva meglesz a feketék száma. |
|
| tótumfaktum |
|
Hát, ha annyi nem is...
Mégiscsak jó volt az első végeredmény, csak éppen a részeredmény nem.
a) piros + kék >= 45
b) fehér + kék >= 52
c) fehér + piros >= 35
d) fekete + piros + fehér + kék = 100
kék=44, fekete=21, fehér=34, piros=1 esetén is teljesülnek a feltételek.
Tehát 100 golyót kell kihúzni, hogy biztosan legyen benne mind a négy színből legalább 1 golyóbis.
|
|
| tótumfaktum |
|
Nekem még mindig nem stimmel...  Mi zárja ki hogy a kék 64 darab?... Mi zárja ki hogy a kék 64 darab?...  |
|
|
|
| katáng |
|
Így is húzható a 67 db: 31 kék + 34 fekete + 2 piros
|
|
| Rendes Kis |
|
34 fekete,
21 fehér,
14 piros,
31 kék.
66 golyót tudok úgy húzni, hogy ne legyen közöttük fekete.
Ha 67-et húzok, abban már biztosan lesz mind a 4 féle szín. |
|
|
|
|
| tótumfaktum |
|
|
Az nem elég ha pl. csak 2 piros és 2 fehér golyó van a zsákban. |
|
|
| tótumfaktum |
|
Hát, nemtom, lehet hogy valamit nem vettem figyelembe, de nekem az jön ki,
hogy a fekete=47, piros=1, kék=51, fehér=1 felállás is teljesíti a feltételeket,
emiatt viszont mind a 100 golyóbist ki kell húzni ahhoz, hogy biztosan legyen benne minden színből legalább 1 pici darabocska, nem?... 
|
|
| tótumfaktum |
|
Nem jó.
Az "alma"=10, "banán"=1, "kókusz"=2
Csak így jön ki helyesen az 1+10+3=14
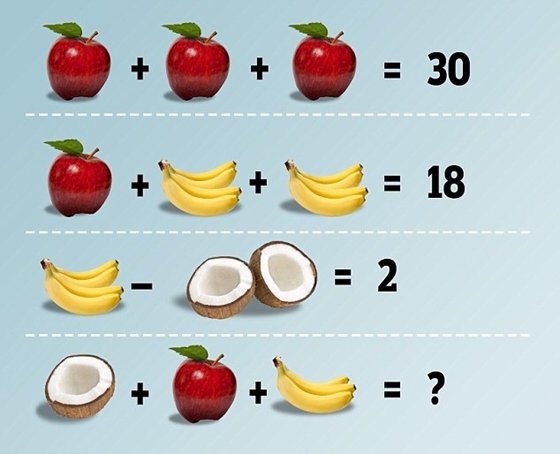
|
|
| katáng |
|
Egy zsákban fekete, fehér, piros, kék golyókat helyeztünk, összesen 100 darabot. A zsákban lévő golyókról a következőket tudjuk:
a) 45 golyó nem fekete és nem is fehér;
b) 52 golyó nem fekete és nem is piros;
c) 35 golyó nem fekete és nem is kék.
Hány golyót kell becsukott szemmel kihúzni a zsákból ahhoz, hogy biztosan legyen mind a négy színű golyóból a kihúzottak között?
|
|
|
| negyven rabló |
|
Na, na!
Nincs félkókusz! 
Idézet:
Á, itt biztos van valami ravaszság!
sztem:
első sor: 3x1 alma = 30, vagyis 10/db
második sor: 1 alma/10 + 8 banán/1, vagyis 1 banán = 1
harmadik sor: 4 banán minusz 2 kókusz= 2, tehát egy kókusz =1
utolsó sor: 1+10+3=14
Jó?
|
|
| Omniscient |
|
Nem, nem, mert akkor meg nem írhatnád ezt a levezetésben:
"harmadik sor: 4 banán minusz 2 kókusz= 2, tehát egy kókusz =1"
hanem, akkor így lenne esetleg helyes a szöveg:
harmadik sor: 4 banán minusz 2 félkókusz= 2, tehát egy félkókusz =1

Azért nem feltűnő, mert a negyedik sorba már nem írtál szöveget ... 
|
|
| negyven rabló |
|
Sztem nincs fél kókusz. Darab van, mint ahogy darab a banán is!
Na mindegy! Tévedhettem is, de tetszett.  |
|
| menta |
|
|
hű, tényleg! ez jó! |
|
| Omniscient |
|
Valójában nem azonos értékűek azok sem. (Ez a másik "csel"  ) )
A Rabló úr végeredménye tökéletes, csak a levezetésnél van egy pici pontatlanság...
alma = 10
banán = 1
kókusz =2
Mer'hogy a fél kókusz = 1, az utolsó sorban .. 
|
|
| menta |
|
|
csak egy banánhéjon: ) |
|
| mackó |
|
Na, igazad van, a csomag banánon elcsúsztam ... 
Rabló uram, felületes szemlélő voltam! |
|
| menta |
|
hm, én is pont így dőltem be, mint 45. De a 40/44 a jó. És el is gondolkodtam, miért dőltem be. Mert a banán elfordítottan szerepel és azt nem néztem meg figyelmesen (áá, azt tudom) Látványban állandóan kiegészítjük a tudomásunkkal azt, amit látunk.
Ez az egyik csel, másik kicsit furcsa, hogy a kókusz is, és a banán is 1 értékű. |
|